Table of Contents

This article was originally published on Toptal. I am sincerely grateful for the opportunity!

Writing an Interpreter From Scratch 🔗

How source code becomes a running program is a mistery for lots of people.
"The compiler does it", yes, but how exactly? Where do we even start?

"Everything boils down to ones and zeros".. yes, but how does the source text of a program get become those bits?

Compilers and interpreters both take raw text, parse it, and make sense of it.
A compiler usually takes raw text and makes an output file (an executable usually).
An interpreter doesn't generate any file, it just "interprets" the source code text, evaluates it immediatelly.

Interpreters are a bit simpler, so we will write a very basic interpreter.
It will only do addition and multiplication, but you will learn a lot, don't worry!

An interpreter is a complex program, so it is usually split into multiple stages:

  1. A lexer is the part that turns a sequence of characters (plain text) into a sequence of tokens.
  2. A parser takes that sequence of tokens and produces an abstract syntax tree (AST) of a language.
    The rules by which a parser operates are usually specified by a formal grammar.
  3. An interpreter is then interprets the AST of the program.

The user code will look something like this:

val input = "2 * 7 + 5"
val tokens = Lexer(input).lex()
val ast = Parser(tokens).parse()
val res = Interpreter(ast).interpret()
println(s"Result is: $res")

We expect it to calculate a final value and print Result is: 19.

The full source code is available at GitHub repo.

Part 1: Writing a Lexer 🔗

Let's say we want to lex this nonsense string: "123 + 45 true * false1".
We are only interested into collecting all tokens in it, nothing else.
It contains different types of tokens:

Whitespace between tokens will be skipped in this example.

At this stage, expressions don't have to make sense; the lexer simply converts the input string into a list of tokens.
The job of "making sense of tokens" is left for the parser.

We'll use this code to represent a token:

case class Token(
  tpe: Token.Type,
  text: String,
  startPos: Int
)

object Token:
  enum Type:
    case Num
    case Plus
    case Times
    case Identifier
    case True
    case False
    case EOF

Every token has a type, textual representation, and position in the original input.
The position helps with debugging. Here it is only index, but usually it contains file name and line number too.

The EOF token is a special token that marks the end of input. It doesn't exist in the source text; we only use it to simplify the parser implementation.

This will be the output of our lexer:

Lexing input:
123 + 45 true * false1

Tokens:
List(
  Token(tpe = Num, text = "123", startPos = 0),
  Token(tpe = Plus, text = "+", startPos = 4),
  Token(tpe = Num, text = "45", startPos = 6),
  Token(tpe = True, text = "true", startPos = 9),
  Token(tpe = Times, text = "*", startPos = 14),
  Token(tpe = Identifier, text = "false1", startPos = 16),
  Token(tpe = EOF, text = "<EOF>", startPos = 22)
)

Let's examine the implementation:

class Lexer(input: String):

  def lex(): List[Token] =
    val tokens = mutable.ArrayBuffer.empty[Token]
    var currentPos = 0
    while currentPos < input.length do
      val tokenStartPos = currentPos
      val lookahead = input(currentPos)
      if lookahead.isWhitespace then
        currentPos += 1 // ignore whitespace
      else if lookahead == '+' then
        currentPos += 1
        tokens += Token(Type.Plus, lookahead.toString, tokenStartPos)
      else if lookahead == '*' then
        currentPos += 1
        tokens += Token(Type.Times, lookahead.toString, tokenStartPos)
      else if lookahead.isDigit then
        var text = ""
        while currentPos < input.length && input(currentPos).isDigit do
          text += input(currentPos)
          currentPos += 1
        tokens += Token(Type.Num, text, tokenStartPos)
      else if lookahead.isLetter then // first must be letter
        var text = ""
        while currentPos < input.length && input(currentPos).isLetterOrDigit do
          text += input(currentPos)
          currentPos += 1
        val tpe = text match
          case "true"  => Type.True // special casing literals
          case "false" => Type.False
          case _       => Type.Identifier
        tokens += Token(tpe, text, tokenStartPos)
      else
        error(s"Unknown character '$lookahead' at position $currentPos")

    tokens += Token(Type.EOF, "<EOF>", currentPos) // special end marker
    tokens.toList

We start with an empty list of tokens, then we go through the string and add tokens as they come.

We use the lookahead character to decide the type of the next token. Note that the lookahead character is not always the furthest character ahead being examined. Based on the lookahead, we know what the token looks like and use currentPos to scan all of the expected characters in the current token, then add the token to the list:

Now we get to something a bit complicated: identifiers versus literals.
The rule we take here is the longest possible match.
Then we check if it matches a literal. If it does we accept it and continue.
Else it is an identifier.

You could choose a different rule instead of greedy "longest match", this is on you to decide.

Take care when handling operators like < and <=. There you have to look ahead one more character, and see if it's an equals sign (=) before concluding that it is a <= operator. Otherwise, it's just a <.

OK, so our lexer is ready. It has produced a list of tokens.

Part 2: Writing a Parser 🔗

We have to give some structure to our tokens—we can't do much with a list alone.
For example, we need to know:

A tree structure supports nesting and ordering. But first, we have to define some rules for constructing these trees.
We need our parser to be unambiguous — to always return the same structure for a given input.
For this we need a formal grammar, which specifies the rules of our parser.

Please note that the following grammar does not follow the previous lexer example!
This grammar is for adding numbers, it has only two tokens, '+' and NUM:

expr = expr '+' expr
expr = NUM

NUM token here means a nonnegative integer, we take it for granted.

Tokens are sometimes called "terminals" in literature.
The intermediate rules are called "nonterminals" (like "expr" in this example).

An equivalent grammar can be written more concise with the pipe symbol (|).
You can read it as "OR" (like in regular expressions):

expr = expr '+' expr | NUM

Either way, we have two rules:

There are many ways we could implement this parser.
We will use a "recursive descent" parsing technique.
It's the most common technique because it is simple to understand and implement.

A recursive descent parser uses one function for each nonterminal in the grammar. It starts from the root rule and goes down from there (hence "descent"), figuring out which rule to apply in each function. The "recursive" part is vital because we can nest nonterminals recursively!

A parser for the first rule would look something like this:

def expr() = 
  expr()
  eat('+')
  expr()

The eat() function checks if the lookahead matches the expected token and then moves the lookahead index.

Unfortunately, we have a few issues with this grammar.
Let's see how to fix them.

Grammar Ambiguity 🔗

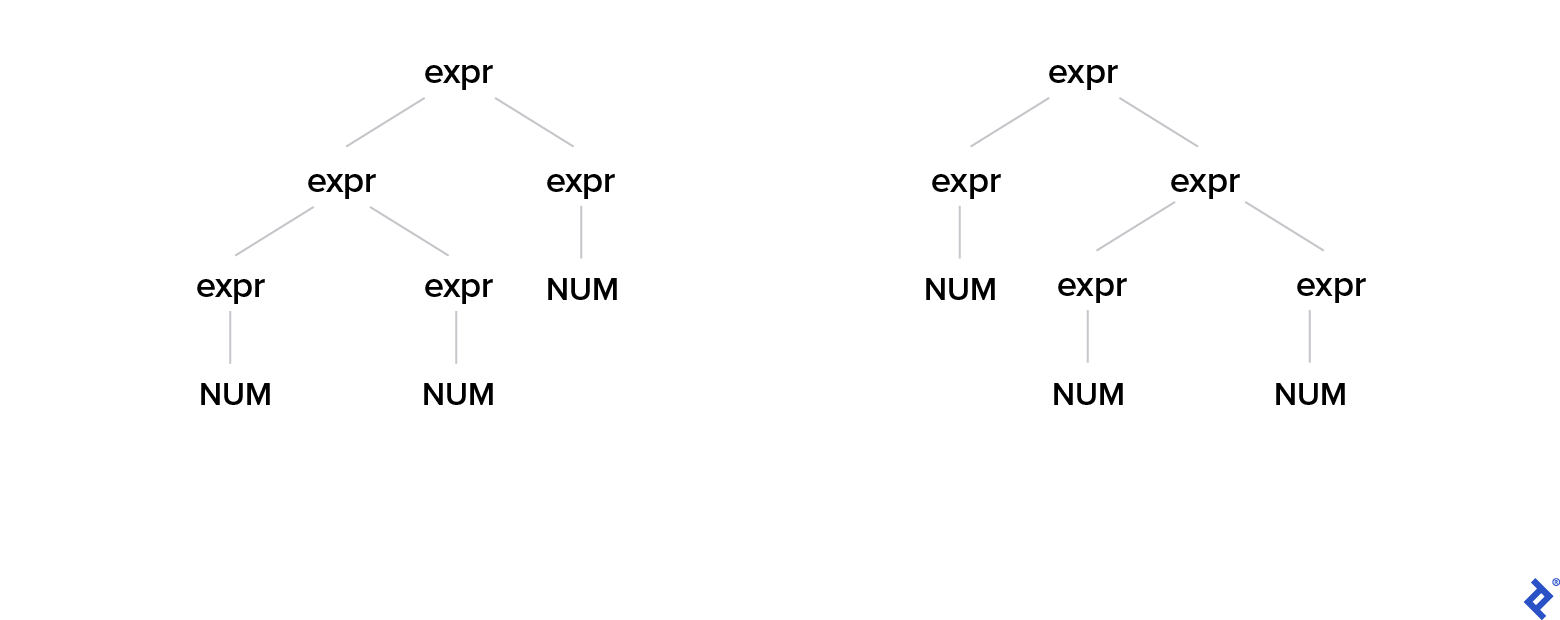
The first issue is the ambiguity of our grammar, which may not be apparent at first glance:

expr = expr '+' expr | NUM

Given the input 1 + 2 + 3, our parser could choose to first make the left expr - or the right expr in the resulting AST:

Two abstract syntax trees. Both start with expr and branch left and right each to another expr, one of which branches straight down to a NUM, and the other of which branches left and right each to another expr that branches down to a NUM. The AST on the left has the larger subtree on its left expr, whereas the AST on the right has the larger subtree on its right expr.

This is why we need to introduce some asymmetry:

expr = expr '+' NUM | NUM

Now this grammar is unambiguous! The parser always goes left, just what we needed! This makes our + operation left associative, but this will become apparent later.

Not the set of expressions we can represent with this grammar has not changed!

Left-recursive Rules 🔗

Unfortunately, the above fix doesn't solve our other problem, left recursion:

def expr() =
  expr()
  eat('+')
  eat(NUM)

We have infinite recursion here. If we were to step into this function, we'd eventually get a stack-overflow error.
Parsing theory to the rescue!

Suppose we have a grammar like this, where alpha could be any sequence of terminals and nonterminals:

A = A alpha | B

We can rewrite this grammar as:

A   = B A'
A'  = alpha A' | epsilon

There, epsilon is an empty string—nothing, no token.

Let's see again our grammar:

expr = expr '+' NUM | NUM

Following the method above, with alpha being the '+' NUM tokens, our grammar becomes:

expr    = NUM exprOpt
exprOpt = '+' NUM exprOpt | epsilon

Finally the grammar is OK, and we can parse it with a recursive descent parser!
Let's see how it looks like:

class Parser(allTokens: List[Token]):
  import Token.Type
  
  private var tokens = allTokens
  private var lookahead = tokens.head
  
  def parse(): Unit = 
    expr()
    if lookahead.tpe != Type.EOF then
      error(s"Unknown token '${lookahead.text}' at position ${lookahead.startPos}")

  private def expr(): Unit =
    eat(Type.Num)
    exprOpt()
  
  private def exprOpt(): Unit =
    if lookahead.tpe == Type.Plus then
      eat(Type.Plus)
      eat(Type.Num)
      exprOpt()
    // else: end recursion, epsilon
  
  private def eat(tpe: Type): Unit =
    if lookahead.tpe != tpe then
      error(s"Expected: $tpe, got: ${lookahead.tpe} at position ${lookahead.startPos}")
    tokens = tokens.tail
    lookahead = tokens.head

Full code is available (at GitHub repo)

The EOF token helps to simplify our parser. We are always sure that there is at least one token in our list (even if file/source is empty), so we don't need to handle the special case of an empty list.

Also, if we switch to a streaming lexer, we wouldn't have an in-memory list but an iterator, so we need a marker to know when we come to the end of the input. When we consume all the tokens, the EOF token should be the last token remaining.

Walking through the code, we can see that an expression can be just a number. If there's nothing left, the next token wouldn't be a Plus, so we would stop parsing. The last token would be EOF, and we would be done.

If the input string has more tokens, then these would have to look like + 123. That's where recursion on exprOpt() kicks in!

Generating an AST 🔗

Now that we successfully parsed our expression, it's hard to do anything with it as is. We could put some callbacks in our parser, but that would be very cumbersome and unreadable. Instead, we will return an AST, a tree representing the input expression:

case class Expr(num: Int, exprOpt: ExprOpt)

enum ExprOpt:
  case Opt(num: Int, exprOpt: ExprOpt)
  case Epsilon

This resembles our rules, using simple data classes.

Our parser now returns a useful data structure:

class Parser(allTokens: List[Token]):
  import Token.Type
  
  private var tokens = allTokens
  private var lookahead = tokens.head
  
  def parse(): Expr = 
    val res = expr()
    if lookahead.tpe != Type.EOF then
      error(s"Unknown token '${lookahead.text}' at position ${lookahead.startPos}")
    else
      res

  private def expr(): Expr =
    val num = eat(Type.Num)
    Expr(num.text.toInt, exprOpt())
  
  private def exprOpt(): ExprOpt =
    if lookahead.tpe == Type.Plus then
      eat(Type.Plus)
      val num = eat(Type.Num)
      ExprOpt.Opt(num.text.toInt, exprOpt())
    else
      ExprOpt.Epsilon

For eat(), error(), and other implementation details, please see the accompanying GitHub repo.

Simplifying Rules 🔗

Our ExprOpt nonterminal can still be improved:

'+' NUM exprOpt | epsilon

It's hard to recognize the pattern it represents in our grammar just by looking at it. It turns out that we can replace this recursion with a simpler construct:

('+' NUM)*

This construct simply means '+' NUM occurs zero or more times.

Now our full grammar looks like this:

expr  = NUM exprOpt*
exprOpt = '+' NUM

And our AST looks nicer:

case class Expr(num: Int, exprOpts: Seq[ExprOpt])
case class ExprOpt(num: Int)

The resulting parser is the same length but simpler to understand and use. We've eliminated Epsilon, which is now implied by starting with an empty list.

We didn't even need the ExprOpt class here. We could have just put case class Expr(num: Int, exprOpts: Seq[Int]), or in grammar format, NUM ('+' NUM)*. So why didn't we?

Consider a case with multiple operators, like - or *, then we'd have a grammar like this:

expr  = NUM exprOpt*
exprOpt = [+-*] NUM

In this case, the AST then needs ExprOpt to specify the operator type:

case class Expr(num: Int, exprOpts: Seq[ExprOpt])
case class ExprOpt(op: String, num: Int)

Note that the [+-*] syntax in the grammar means the same thing as in regular expressions: "one of those three characters." We'll see this in action soon.

Part 3: Interpreter 🔗

Our interpreter will make use of our lexer and parser to get the AST of our input expression.
Then it will evaluate that AST however we want. In this case, we're dealing with numbers, and we want to evaluate their sum.

In the implementation of our interpreter example, we will use this simple grammar:

expr  = NUM exprOpt*
exprOpt = [+-] NUM

And this AST:

case class Expr(num: Int, exprOpts: Seq[ExprOpt])
case class ExprOpt(op: Token.Type, num: Int)

Let's see how to write an interpreter for the above grammar:

class Interpreter(ast: Expr):

  def interpret(): Int = eval(ast)

  private def eval(expr: Expr): Int =
    var tmp = expr.num
    expr.exprOpts.foreach { exprOpt =>
      if exprOpt.op == Token.Type.Plus
      then tmp += exprOpt.num
      else tmp -= exprOpt.num
    }
    tmp

If we parsed our input into an AST successfully, we'll always have at least one NUM. Then we take the optional numbers and add them to (or subtract them from) our result.

The note from the beginning about the left associativity of + is now clear: We start from the leftmost number and add others, from left to right. This may seem unimportant for addition, but consider subtraction: The expression 5 - 2 - 1 is evaluated as (5 - 2) - 1 = 3 - 1 = 2 and not as 5 - (2 - 1) = 5 - 1 = 4!

But if we want to go beyond interpreting plus and minus operators, there's another rule to define.

Precedence 🔗

We know how to parse a simple expression like 1 + 2 + 3, but when it comes to 2 + 3 * 4 + 5, we have a bit of a problem.

Most people agree on the convention that multiplication has higher precedence than addition. But the parser doesn't know that. We can't just evaluate it as ((2 + 3) * 4) + 5. Instead we want (2 + (3 * 4)) + 5.

This means that we need to evaluate multiplication first. Multiplication needs to be further from the root of the AST to force it to be evaluated before addition. For this, we need to introduce yet another layer of indirection.

Final Grammar Version 🔗

We start from a naive, left-recursive grammar, which has no precedence rules:

expr = expr '+' expr | expr '*' expr | NUM

First, we give it rules of precedence and remove its ambiguity:

expr    = expr '+' term | term
term    = term '*' NUM | NUM

As you can see, we just invented a new nonterminal called "term" here.
This is just so we push the multiplication deeper into the tree.

Then we remove the left-recursive rules:

expr      = term exprOpt*
exprOpt   = '+' term
term      = NUM termOpt*
termOpt   = '*' NUM

The result is a beautifully expressive AST:

case class Expr(term: Term, exprOpts: Seq[ExprOpt])
case class ExprOpt(term: Term)

case class Term(num: Int, termOpts: Seq[TermOpt])
case class TermOpt(num: Int)

This leaves us with a concise interpreter implementation:

class Interpreter(ast: Expr):

  def interpret(): Int = eval(ast)

  private def eval(expr: Expr): Int =
    var tmp = eval(expr.term)
    expr.exprOpts.foreach { exprOpt =>
      tmp += eval(exprOpt.term)
    }
    tmp

  private def eval(term: Term): Int =
    var tmp = term.num
    term.termOpts.foreach { termOpt =>
      tmp *= termOpt.num
    }
    tmp

Regexes 🔗

You might ask "What about regexes?", how do they fit in all of this?
Turns out they are not powerful enough to handle recursion, but they can be used for implementing parts of lexer for example. They can't even handle balanced parentheses.

Conclusion 🔗

Writing a parser correctly by hand can be challenging. That's why there are tools like ANTLR, that can generate parsers for many popular programming languages. These are called parser generators.

There are also libraries called parser combinators, that enable you to write parsers directly in your preferred programming language. Examples include FastParse for Scala and Parsec for Python.

In "production code" you should probably start with battle tested generators/combinator.
And later maybe reimplement parts of it if performance degrades.

Next Steps 🔗

We didn't cover this, but error handling and reporting are crucial features of any parser. As developers, we know how frustrating it can be when a compiler produces confusing or misleading errors. It's an area that has many interesting problems to solve, like giving correct and precise error messages, not deterring the user with more messages than necessary, and recovering gracefully from errors. It's up to the developers writing an interpreter or compiler to ensure their future users have a better experience.

In our example lexers, parsers, and interpreters, we only scratched the surface of the theories behind compilers and interpreters. Other important topics are:

For further reading, I recommend these resources: